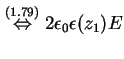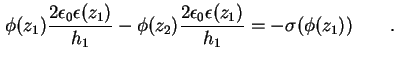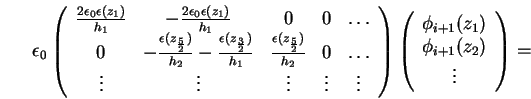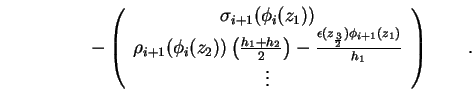Diskretisierung
Bei der numerischen Lösung von Differentialgleichungen wird der Träger der gesuchten Lösung zerlegt
in finite Differenzen [Sel84]. Unser Modell ist eindimensional, daß heißt, das Bauteil hat nur zwei
Oberflächen: den linken Rand
Da im Gegensatz zu einer analytischen Lösung, die auf einem kontinuierlichen
Träger lebt, die numerische Lösung auf einer endlichen Anzahl von Stützstellen gegeben ist, müssen
die Werkzeuge der Infinitesimalrechnung entsprechend modifiziert werden. Bei der Ableitung einer
Funktion
mit dem Index der Stützstellen m und dem Abstand zweier Stützstellen
Zum Lösen der Poisson-Gleichung (1.10) wird diese über jeweils eine Stützstelle
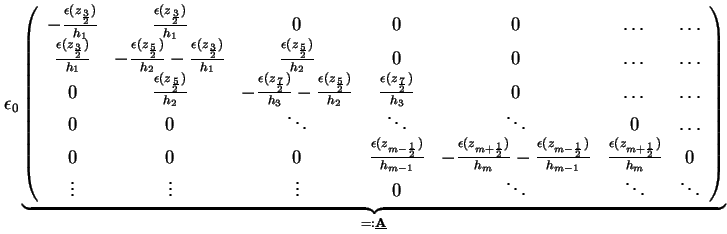
Dadurch läßt sich der diskretisierte, eindimensionale Laplace-Operator in Matrixform darstellen
Zusammen mit dem Vektoren
wobei n die Zahl der Stützstellen ist, läßt sich die eindimensionale Poisson-Gleichung (1.10)
für den Iterationsschritt
Die Matrix
Um schnell, also mit minimaler Anzahl an Iterationsschritten, eine konvergierte Lösung zu erhalten, wird
das Newton-Verfahren eingesetzt (Abschnitt 1.5.1). Für den neuen Differential-Operator
und daraus
wobei die Rechnung zur Ableitung des Fermi-Dirac-Integrals in Anhang C zu finden ist.
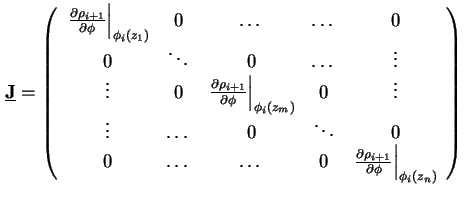
Unter Verwendung der Jakobi-Matrix
wird die diskretisierte Poisson-Gleichung (1.66) für das Newton-Verfahren modifiziert Es müssen nun noch die Randbedingungen verwendet werden. Aus der Dirichlet-Randbedingung für die Poisson-Gleichung (1.8) folgt
wobei
Die ersten beiden Zeilen des Gleichungssystems (1.66) schreiben sich für die
Dirichlet-Randbedingung damit um zu
Analog folgt für die letzten beiden Zeilen
mit
Bei der Neumann-Randbedingung (1.9) ist die Ableitung des Potentials, also das Feld E, am
Rand durch die Oberflächenladung
Unter der Annahme, daß am Ort L der Potentialverlauf spiegelsymmetrisch ist (siehe Abbildung
1.5, vergleiche gegebenenfalls mit Abbildung 3.3), folgt für das
innere Feld und damit
Durch stückweise Integration der Poisson-Gleichung (1.10) über den linken Rand findet
man
Das und verwenden von (1.80) ergibt
Somit schreiben sich die ersten beiden Zeilen des Gleichungssystems (1.66) für die
Neuman-Randbedingung um zu
Ein Verfahren zur Lösung der Strom-Gleichungen ist in Abschnitt 1.5.2 ausführlich besprochen worden. Zusammen mit diesem Algorithmus und der Definition des Integrals auf diskreten Stützstellen (1.60) können damit die Quasi-Fermi-Niveaus berechnet werden. |
![\includegraphics[draft=false, height=12cm, angle=270]{bilder/inhomogGitter.epsi}](img256.png)
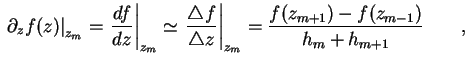
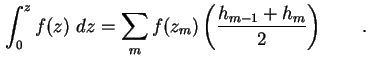
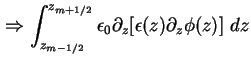
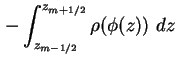
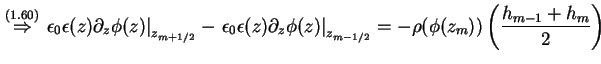
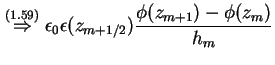
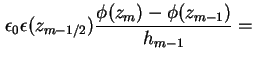
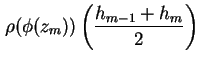
![$\displaystyle \Leftrightarrow
\epsilon_0 \epsilon (z_{m-1/2}) \frac{\phi(z_{m-1...
...ac{ \epsilon (z_{m+1/2})}{h_{m}}
+ \frac{\epsilon (z_{m-1/2})}{h_{m-1}} \right]$](img273.png)
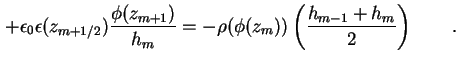
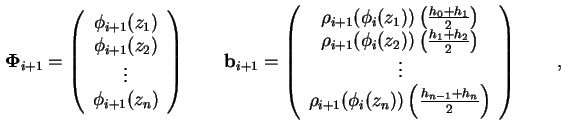
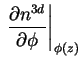
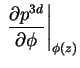
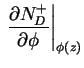
![$\displaystyle - e \beta \frac{N_D (z) 2 exp(\beta[E_{Fn}(z) - E_D(z)])}{(1 + 2 exp(\beta[E_{Fn}(z) - E_D(z)]))^2}$](img291.png)
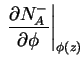
![$\displaystyle e \beta \frac{N_A (z) 4 exp(\beta[E_A(z) - E_{Fp}(z)])}{(1 + 4 exp(\beta[E_A(z) - E_{Fp}(z)]))^2} \qquad,$](img293.png)
![$\displaystyle \left. \frac{\partial \rho}{\partial \phi} \right\vert _{\phi ( z...
...) }
+ \left. \frac{\partial N_D^+}{\partial \phi}\right\vert _{\phi ( z ) }
] ,$](img294.png)
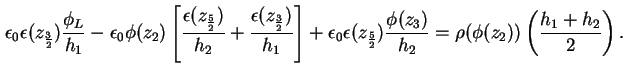
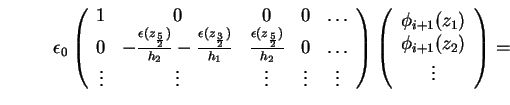
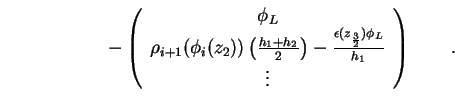
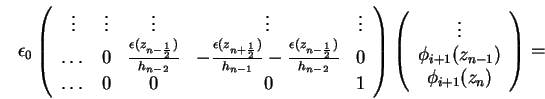
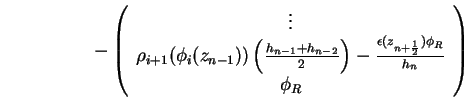
![\includegraphics[draft=false, width=7cm, angle=270]{bilder/RandbedNeum.epsi}](img307.png)
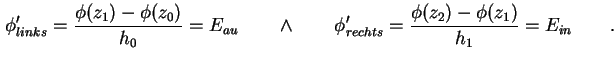
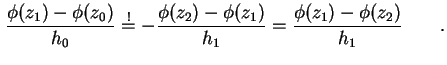
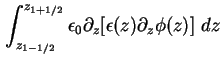
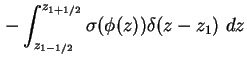
![$\displaystyle \Rightarrow \epsilon_0 \epsilon(z_1) \left[ \partial_z \left. \phi \right\vert _{z_{3/2}} - \partial_z \left. \phi \right\vert _{z_{1/2}} \right]$](img315.png)