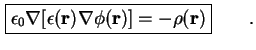|
| (1.3) |
Es gelten die Bezeichnungen: für die elektrische Feldkonstante
![]() , die Ladungsträgerdichte
, die Ladungsträgerdichte
![]() , die dielektrische Verschiebung
, die dielektrische Verschiebung
![]() und die Polarisation
und die Polarisation
![]() .
.
Mit der ortsabhängigen, relativen Dielektrizitätskonstante
![]() schreibt sich die
dielektrische Verschiebung
schreibt sich die
dielektrische Verschiebung
![]() als
als
Aus (1.1) folgt die Existenz eines skalaren Potentials
![]() [Wüs95, Satz 18.10
und Satz 18.12]
[Wüs95, Satz 18.10
und Satz 18.12]
Dieses eingesetzt in (1.4) zusammen mit (1.2) ergibt die Poisson-Gleichung der
klassischen Elektrodynamik mit einer ortsabhängigen, relativen Dielektrizitätskonstante
![]()
Die Ladungsdichte (pro ![]() )
)
![]() in einem Halbleiterbauelement setzt sich zusammen aus
der Ladungsträgerdichte der freien Elektronen
in einem Halbleiterbauelement setzt sich zusammen aus
der Ladungsträgerdichte der freien Elektronen
![]() , schweren Löchern
, schweren Löchern
![]() und leichten Löchern
und leichten Löchern
![]() , sowie den Dichten der ionisierten Akzeptoren
, sowie den Dichten der ionisierten Akzeptoren
![]() und Donatoren
und Donatoren
![]() . Es gilt
. Es gilt
mit der Elementarladung ![]() und
und
![]() .
.
Bei Gleichung (1.6) handelt es sich um eine Differentialgleichung zweiter Ordnung,
für eine eindeutige Lösung werden Randbedingungen auf der Oberfläche
![]() des Bauelements
benötigt [Wüs95, Satz 24.7]. Diese lassen sich als Dirichlet-Randbedingung (
des Bauelements
benötigt [Wüs95, Satz 24.7]. Diese lassen sich als Dirichlet-Randbedingung (
![]() auf
auf
![]() gegeben)
gegeben)
oder als Neumann-Randbedingung (Normalen-Ableitung von
![]() auf
auf
![]() gegeben)
gegeben)
formulieren. ![]() ist eine Konstante,
ist eine Konstante,
![]() der Normalenvektor
auf der Oberfläche des Bauteils,
der Normalenvektor
auf der Oberfläche des Bauteils,
![]() die Oberflächenladungsdichte (Einheit:
die Oberflächenladungsdichte (Einheit: ![]() ).
Die Dirichlet-Randbedingung liefert ein eindeutiges Potential, bei ausschließlicher Verwendung der
Neumann-Randbedingung bestimmt man das Potential bis auf eine Konstante. Letztere ist unbedeutend, da
sie zum Beispiel bei Gradientenbildung zur eigentlich interessierenden Feldstärke
).
Die Dirichlet-Randbedingung liefert ein eindeutiges Potential, bei ausschließlicher Verwendung der
Neumann-Randbedingung bestimmt man das Potential bis auf eine Konstante. Letztere ist unbedeutend, da
sie zum Beispiel bei Gradientenbildung zur eigentlich interessierenden Feldstärke
![]() wegfällt. Eine physikalisch eindeutige Lösung ist also durch beide Typen von
Randbedingungen festgelegt [Nol97].
wegfällt. Eine physikalisch eindeutige Lösung ist also durch beide Typen von
Randbedingungen festgelegt [Nol97].
Die zu untersuchenden Halbleiterstrukturen mit Quantenpunkten werden schichtweise gewachsen [Bim99], das heißt in Wachstumsrichtung (negative z-Achse) variieren Struktureigenschaften wie verwendeter Materialtyp oder Dotierungskonzentration, lateral sind die Struktureigenschaften konstant. Bei der Beschreibung eines Bauteils wird sich dieser Umstand zu Nutze gemacht, in dem man die eindimensionale Poisson-Gleichung
mit
| (1.11) |
betrachtet. Dies führt zu einer erheblichen Reduktion des Rechenaufwands.
Gesetzmäßigkeiten zum Berechnen der Ladungsträgerdichten werden in den folgenden Abschnitten 1.2 und 1.3 abgeleitet.