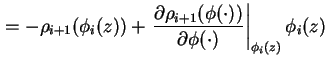|
| (1.40) |
Im nächsten Iterationsschritt ![]() wird mit dem errechneten
wird mit dem errechneten ![]() ein
ein
![]() bestimmt, aus
welchem man wieder durch Invertieren des Laplace-Operators ein
bestimmt, aus
welchem man wieder durch Invertieren des Laplace-Operators ein
![]() bestimmt. Die Iteration
führt man so oft durch, bis das Residuum
bestimmt. Die Iteration
führt man so oft durch, bis das Residuum
unterhalb einer anzugebenden Schranke liegt. Man spricht dann von einer konvergierten Lösung.
Die Definition (1.41) hat den Nachteil, daß man für jede neue Rechnung wieder eine geeignete Schranke ermitteln muß. Vorteilhafter ist es daher, das normierte Residuum
![$\displaystyle Res_{1,i} := \frac{\lVert \left[\epsilon_0 \partial_z \epsilon(z)...
...ial_z \epsilon(z) \partial_z \right]^{-1} \rho_i ( \phi_{i-1} ( z ) ) \rVert_2}$](img216.png) |
(1.42) |
zu verwenden.
Der formale Ablauf des Fixpunktverfahrens erweist sich bei konkreten Rechnungen als unbrauchbar. Der Grund
dafür ist, daß die ersten Iterationsschritte ![]() , aufgrund der starken Nichtlinearität in
(1.39), Werte für
, aufgrund der starken Nichtlinearität in
(1.39), Werte für ![]() liefern, die sehr weit weg von der gesuchten Lösung liegen.
liefern, die sehr weit weg von der gesuchten Lösung liegen.
Eine Möglichkeit zur Verfeinerung des Fixpunktverfahrens ist das sogenannte Dämpfen, bei dem man
jeder neuen Lösung
![]() grundsätzlich einen sehr großen Fehler unterstellt und sie daher
mit der vorangegangen Lösung
grundsätzlich einen sehr großen Fehler unterstellt und sie daher
mit der vorangegangen Lösung ![]() vermengt
vermengt
| (1.43) |
Mit dem Faktor
![]() gewichtet man den Einfluß der neuen Lösung
gewichtet man den Einfluß der neuen Lösung
![]() .
Für
.
Für
![]() verschwindet der Einfluß der vorangegangen Lösung
verschwindet der Einfluß der vorangegangen Lösung ![]() , für
, für
![]() dämpft man den Einfluß von
dämpft man den Einfluß von
![]() und
und
![]() übergewichtet den Einfluß von
übergewichtet den Einfluß von
![]() .
.
Eine Möglichkeit zur Beschleunigung der Konvergenz ist das Newton-Verfahren. Im Gegensatz zum
Fixpunktverfahren wird hier die Ladungsträgerdichte
![]() nach
nach ![]() bis zur ersten Ordnung
Taylor-entwickelt [Bro81] und damit Laplace-Operator und Inhomogenität in der Poisson-Gleichung
modifiziert [Sel84]. Das heißt, für ein Potential
bis zur ersten Ordnung
Taylor-entwickelt [Bro81] und damit Laplace-Operator und Inhomogenität in der Poisson-Gleichung
modifiziert [Sel84]. Das heißt, für ein Potential ![]() des Iterationsschritts
des Iterationsschritts ![]() schreibt
sich (1.39) im folgenden Iterationsschritt
schreibt
sich (1.39) im folgenden Iterationsschritt ![]() zu
zu
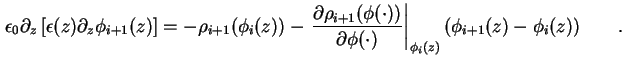 |
(1.44) |
Die so umgeformte Poisson-Gleichung
wird mit ihrem neuen Differentialoperator-Operator
![]() und neuer Inhomogenität dem
Fixpunkt-Verfahren unterzogen. Als Faustregel gilt, daß wenn das Fixpunkt-Verfahren eine Lösung findet,
das Newton-Verfahren diese in den meisten Fällen schneller findet. Scheitert das Fixpunkt-Verfahren, so
findet auch das Newton-Verfahren keine Lösung. Der Vorteil beschränkt sich also auf die Rechenzeit
[Sel84], [Meh01]. Unter anderem für hohe Temperaturen (
und neuer Inhomogenität dem
Fixpunkt-Verfahren unterzogen. Als Faustregel gilt, daß wenn das Fixpunkt-Verfahren eine Lösung findet,
das Newton-Verfahren diese in den meisten Fällen schneller findet. Scheitert das Fixpunkt-Verfahren, so
findet auch das Newton-Verfahren keine Lösung. Der Vorteil beschränkt sich also auf die Rechenzeit
[Sel84], [Meh01]. Unter anderem für hohe Temperaturen (![]() ) hat sich das
Newton-Verfahren bei der Simulation von Halbleiterbauelementen bewährt.
) hat sich das
Newton-Verfahren bei der Simulation von Halbleiterbauelementen bewährt.
![$\displaystyle \underbrace{\left[ \epsilon_0 \partial_z \epsilon ( z ) \partial_...
...\cdot )} \right\vert _{\phi_{i}(z)}\right]}_{=: \tilde \Delta} \phi_{i+1} ( z )$](img224.png)