|
![\includegraphics[draft=false, width=11.3cm]{bilder/schottkyneu.eps}](img182.png) |
Für den Wert des Potentials
![]() am Ort des Schottky-Kontakts im Gleichgewicht (markiert durch den
Index ,,0``,
am Ort des Schottky-Kontakts im Gleichgewicht (markiert durch den
Index ,,0``, ![]() und
und ![]() sind der spätere linke und rechte Rand des eindimensionalen Modells) bedeutet das,
hier exemplarisch für das Leitungsband,
sind der spätere linke und rechte Rand des eindimensionalen Modells) bedeutet das,
hier exemplarisch für das Leitungsband,
![]() und
und
![]() sind Materialparameter. Durch geeignete Wahl des Nullpunkts der Energie, zum
Beispiel
sind Materialparameter. Durch geeignete Wahl des Nullpunkts der Energie, zum
Beispiel 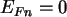 , läßt sich eine Randbedingung für
, läßt sich eine Randbedingung für ![]() formulieren. Der Abstand Bandkante zum
Quasi-Fermi-Niveau am Schottky-Kontakt ist festgelegt durch die Höhe der Schottky-Barriere
formulieren. Der Abstand Bandkante zum
Quasi-Fermi-Niveau am Schottky-Kontakt ist festgelegt durch die Höhe der Schottky-Barriere ![]() . Feste
Werte sind also
. Feste
Werte sind also ![]() ,
, ![]() ,
, ![]() , durch (1.36) ist damit eine
Dirichlet-Randbedingung für die Poisson-Gleichung (1.8) am Schottky-Kontakt gegeben.
, durch (1.36) ist damit eine
Dirichlet-Randbedingung für die Poisson-Gleichung (1.8) am Schottky-Kontakt gegeben.
Alternativ gibt es den Ohm'schen Kontakt, der sich als Schottky-Kontakt mit vernachlässigbar kleinem
Übergangswiderstand definiert, das heißt Ladungsträger können vom Metall in den Halbleiter
gehen und wieder zurück. Dies erreicht man durch eine entsprechend geringe Austrittsarbeit ![]() des
Metalls (materialspezifisch) und/oder durch hohes Dotieren des Halbleiters - siehe Abbildung
1.2. Bei einem kleinen
des
Metalls (materialspezifisch) und/oder durch hohes Dotieren des Halbleiters - siehe Abbildung
1.2. Bei einem kleinen ![]() können die Elektronen das Metall aufgrund thermischer
Anregung verlassen. Dotiert man den Halbleiter stark, dann wird die Verarmungsschicht dünner und die
Elektronen können durch die Barriere tunneln [Sze81].
können die Elektronen das Metall aufgrund thermischer
Anregung verlassen. Dotiert man den Halbleiter stark, dann wird die Verarmungsschicht dünner und die
Elektronen können durch die Barriere tunneln [Sze81].
![\includegraphics[draft=false, width=7cm, angle=270]{bilder/ohmkontakt.epsi}](img188.png) |
Als Dirichlet-Randbedingung (1.8) für
![]() am Ort des Ohm'schen Kontakts formuliert
sich im Gleichgewicht bei geeigneter Wahl des Nullpunkts der Energie, zum Beispiel wieder
am Ort des Ohm'schen Kontakts formuliert
sich im Gleichgewicht bei geeigneter Wahl des Nullpunkts der Energie, zum Beispiel wieder 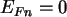 ,
aus der geforderten Ladungsneutralität, hier exemplarisch für das Leitungsband,
,
aus der geforderten Ladungsneutralität, hier exemplarisch für das Leitungsband,
| (1.37) |
Mit der Konvention, daß die Spannung ![]() zu gleichen Teilen an beiden Kontakten angelegt wird, folgt
für das Nicht-Gleichgewicht
zu gleichen Teilen an beiden Kontakten angelegt wird, folgt
für das Nicht-Gleichgewicht
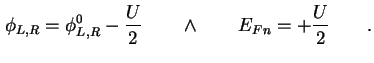 |
(1.38) |