Stichwörter
Wolfram Documentation
Wolfram Information

Informationen

Einführung

Mathematicaliz.
webMathematica
gridMathematica

Zusatzpakete
German Language
Wolfram Workbench

Publicon
Player Pro

Bücher

Support

Service | Update
Transfer

Lizenzen

Einblicke

Tech Tipps
Beispiele | News
Mathematica testen

The cuboid correlation function1.nb

Beispiel 1 | Besipiel 2 | Besipiel 3 | Beispiel 4

By C. Herrmann & W. Gille, 1999: This is a representation of the structure functions , p(r) and A(l) of a cuboid with edges by means of a Mathematica program.

1. The complete expressions for 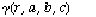. Eight r-intervals are considered and simple checks are performed.
2. An application of the 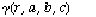expression: Determination of the chord length distribution density A(l,a,b,c) of the cuboid.
3. Plots of 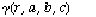, p(r,a,b,c) and A(l,a,b,c) in a special case: Fixed edges a=3, b=4, c=5 are considered.

1.Definitions of the expressions for 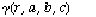and simple checks.

The in the eight r-intervals are defined.

Display of all gama terms

All the -terms are available in detail. Each term is restricted to a certain r-interval. Eight r-intervals are necessary. In these expressions no abbreviations are used.

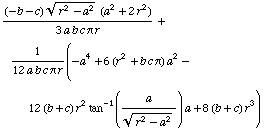
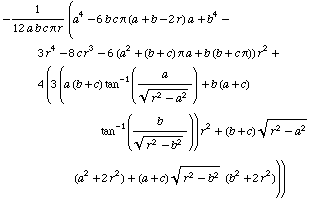
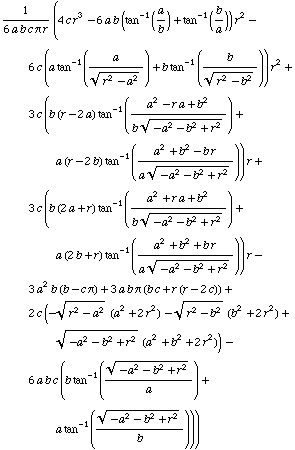
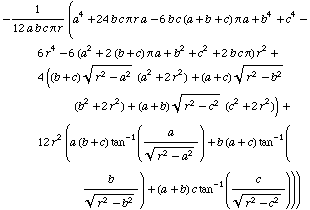
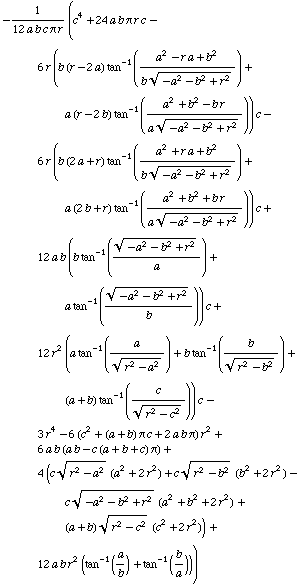
A test is performed to check the definition

The space diagonal L is the largest dimension of the cuboid. holds. Analytically this can be shown by the following lines. Here, exclusively the expression gama7 is used.

Similarly, it can be shown, that is a continuous function. All endpoints of the r-intervals, for example , must be considered then.

2. Determination of the chord length distribution density A(l,a,b,c) of the cuboid

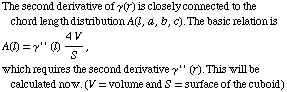
All A-terms are restricted to certain r-intervals. Based on , again, eight r-intervals are necessary.

Now, the definition of A(l,a,b,c) in all possible l-intervals.

This is a test of the normalization of the chord length distribution in a case a=1, b=2, c=3. The theoretical result is 1.0

3. Plots of , A(l,a,b,c) and p(r,a,b,c)

First, the graphical representation of a cuboid is defined.

Next, a graphical combination of cuboid , correlation function and the chord length distribution density is constructed.

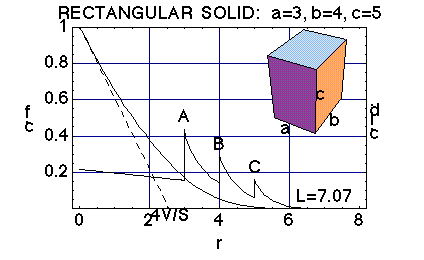
Fig. 1: The correlation function (c.f.) and the chord length distribution density (c.l.d.) of a cuboid The positions of the three spikes A, B, C in the chord length distribution clearly mark the edges a,b,c of the cuboid.

On the other hand, the maximum particle dimension cannot be detected via A(l,a,b,c).

The correlation function is a continuous function in the whole r-interval . holds, if .

Finally the distance distribtion densities of cuboid and sphere are compared.

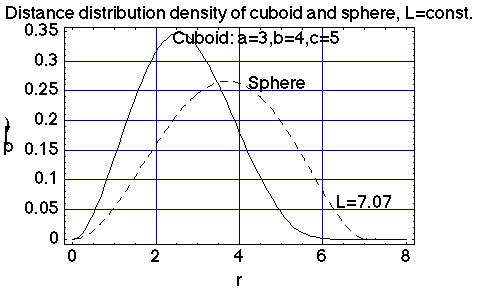
Fig. 2: The p(r) function of a cuboid and of a sphere with the same maximum dimension L The length cannot be detected exactly in such a plot.

In the case of a spherical particle, the L-estimation can be handled by differentiation of . This method does not work in the cuboid case. Here, the L-estimation is relatively complicated.

This is a consequence of the corners of this geometric figure.