|
|||||
|
Firma | Mathematik | Naturwissenschaft & Technik | Schule | Simulation | Programmieren | Bücher | Sonstiges | Dienstleistungen |
|||||
Mathematica - Statistische Anwendung |
 |
Beispiel 1 | Beispiel 2 | Beispiel 3 | Beispiel 4
Dieses Notebook wurde verfasst von Carsten Herrmann.
Es demonstriert zum einen die grundsätzliche Einsatzmöglichkeit von Mathematica zum Verfassen von lebendigen mathematisch-technischen Abhandlungen, insbesondere aber auch die Konvertierung in HTML (d.h. das "Notebook" - Bezeichnung der Mathematica-Dateien - wurde mit Mathematica erstellt und in Mathematica anschließend im HTML-Format abgespeichert).
Das Thema des Notebooks entspricht der Ausbildung des Verfassers, zum Inhalt selber werden gerne Anregungen/Korrekturen entgegengenommen.
Regressionen
Als Beispiel diene folgende abstrahierte Situation:
Drei Signale werden getrennt verstärkt (oder abgeschwächt), hinter den drei Signalmultiplikatoren mit unbekannten Verstärkungsfaktoren u, v, w werden die drei Signale addiert.
Quantitativ gefasst :
Dieses Gerät (Verstärker-Addierer) gibt es viermal. Gemessen wird das Summensignal 
bei unterschiedlichen Eingangssignalen, die vier Messgeräte haben unterschiedliche Genauigkeiten (Standardabweichungen).
Gesucht ist eine Schätzung der drei Verstärkungsfaktoren aufgrund folgender Messdaten:
Gerät 1: u + 2w = 4,310.9 Standardabw = 0,000 7
Gerät 2: u + v + 2w = 4,849.8 Standardabw = 0,001 3
Gerät 3: u + 4w = 5,059.4 Standardabw = 0,000 7
Gerät 4: u + v + 4w = 5,594.75 Standardabw = 0,000 10
Lineare Regression
Bei der Linearen Regression geht man eigentlich davon aus, dass die Standardabweichungen gleich sind. Sie werden außer acht gelassen bei dem Modell. y = x Hier wird ß so bestimmt, dass || W ß -y || minimal wird. Der Schätzer für ß hat einen gewissen Erwartungswert und Varianz. Es lässt sich mit den aus der Stichprobe gewonnenen Werten ein Vertrauensbereich errechnen.
Die Varianzanalyse dient der Beurteilung, wieviel von der Gesamtvarianz in y (Abweichungen vom Mittelwert von y) durch die lineare Regression erklärt werden kann und wieviel noch an (unerklärter) Restvarianz verbleibt.
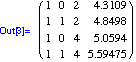
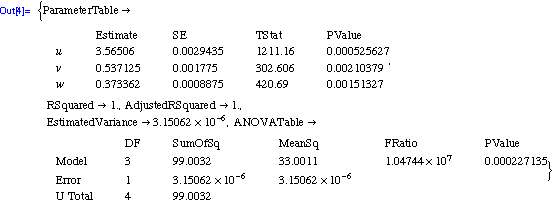
Gauss-Markov ("minimum variance unbiased estimate")
Das Modell ist y = W ß + e , wobei e ein Zufallsvektor (Messfehler) mit Mittelwert Null und Kovarianz E(e 
=Q sei. Der Schätzwert ist dann 
In diesem Beispiel ist
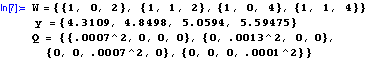
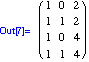
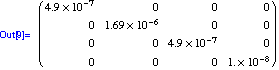
Die Fehler-Kovarianz ist
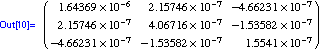
Und der Schätzwert lautet dann
"Minimum-Variance estimate"
Das Modell ist y = W ß + e , wobei ß und e Zufallsvektoren sind. Es soll minimiert werden E 
Allgemein kann man das wohl nicht ohne weitere Angaben lösen. Nimmt man jedoch an, dass E[e 
] = Q und E[ß 
]= R, sowie E[e 
]= 0, R und Q positiv-semi-definit, W R 
+ Q nicht-singulär, dann ist der lineare Min-Varianz Schätzwert von ß 
mit Fehlerkovarianz 
Neu gegenüber den Gauss-Markov Schätzern ist R. Ist 
= 0, dann ist der Minimum-Varianz Schätzwert gleich dem Gauss-Markow-Schätzwert.
top