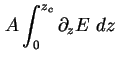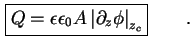Die Ladung Q innerhalb eines zu betrachtenden Volumens V der Heterostruktur ergibt sich nach dem
physikalischen Gauß'schen Satz [Jac75] zu
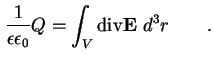 |
(2.16) |
Abbildung 2.5:
Ladungsdichte 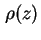 und daraus resultierende Feldstärke
und daraus resultierende Feldstärke 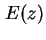 am
am 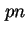 -Übergang.
-Übergang.
![\includegraphics[draft=false, width=10.5cm]{bilder/erhopndiode.epsi}](img383.png) |
Am Ort der Raumladungszone 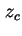 ist die Leitfähigkeit am geringsten, der Widerstand also am größten.
Dieser Bereich wirkt wie ein Isolator, daher wird die Raumladungszone auch Sperrschicht genannt. Gemäß
(1.2) ist
ist die Leitfähigkeit am geringsten, der Widerstand also am größten.
Dieser Bereich wirkt wie ein Isolator, daher wird die Raumladungszone auch Sperrschicht genannt. Gemäß
(1.2) ist 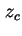 auch der Ort des maximalen Feldes
auch der Ort des maximalen Feldes 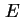 - siehe Abbildung 2.5. Das
Bauteil läßt sich deshalb bei
- siehe Abbildung 2.5. Das
Bauteil läßt sich deshalb bei 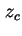 in zwei Leiter zerlegt denken, die beide die Ladung
in zwei Leiter zerlegt denken, die beide die Ladung
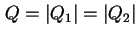 tragen, dargestellt in Abbildung 2.6. Bei einer
tragen, dargestellt in Abbildung 2.6. Bei einer 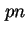 -Diode also
am
-Diode also
am 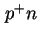 - beziehungsweise
- beziehungsweise 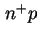 -Übergang und bei der Schottky-Diode am Schottky-Kontakt.
-Übergang und bei der Schottky-Diode am Schottky-Kontakt.
Abbildung 2.6:
Zerlegung des Bauteils in zwei Leiter.
![\includegraphics[draft=false, width=7cm, angle=270]{bilder/SkizzeKapazitaet.epsi}](img386.png) |
Unsere Simulation ist eindimensional, das heißt, daß das Feld 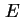 in lateraler Richtung verschwindet,
da dort
in lateraler Richtung verschwindet,
da dort
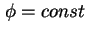 gilt. In der mehrdimensionalen Integralrechnung kann man ein Volumenintegral, hier
(2.16), überführen in ein eindimensionales Integral der stetigen Querschnittsfunktion des zu
integrierenden Volumens, die in diesem Fall gleich der Diodenfläche A ist [Wüs95, Satz 19.10]. Zieht man
die konstante Querschnittsfläche A vor das Integral und integriert bei der
gilt. In der mehrdimensionalen Integralrechnung kann man ein Volumenintegral, hier
(2.16), überführen in ein eindimensionales Integral der stetigen Querschnittsfunktion des zu
integrierenden Volumens, die in diesem Fall gleich der Diodenfläche A ist [Wüs95, Satz 19.10]. Zieht man
die konstante Querschnittsfläche A vor das Integral und integriert bei der 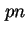 -Diode von dem
Ohm'schen Kontakt (z = 0) hin zu der Raumladungszone (
-Diode von dem
Ohm'schen Kontakt (z = 0) hin zu der Raumladungszone (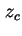 ) beziehungsweise bei der Schottky-Diode
vom Ohm'schen Kontakt (z = 0) zum Schottky-Kontakt (
) beziehungsweise bei der Schottky-Diode
vom Ohm'schen Kontakt (z = 0) zum Schottky-Kontakt (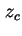 ), so ergibt sich für (2.16)
), so ergibt sich für (2.16)
mit
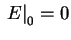 , da das Feld an einem Ohm'schen Kontakt verschwindet.
, da das Feld an einem Ohm'schen Kontakt verschwindet.
Es gilt also [Wet00]
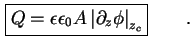 |
(2.20) |
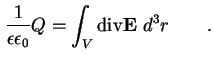
![\includegraphics[draft=false, width=10.5cm]{bilder/erhopndiode.epsi}](img383.png)
![\includegraphics[draft=false, width=7cm, angle=270]{bilder/SkizzeKapazitaet.epsi}](img386.png)