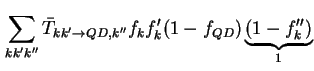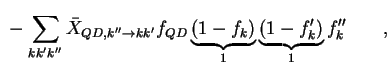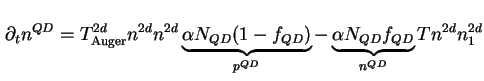|
| (3.1) |
Analog folgt für die Stoßionisation, bei der zwei unbesetzte Zustände ![]() ,
, ![]() im Leitungsband,
ein besetzter Zustand
im Leitungsband,
ein besetzter Zustand ![]() in den Quantenpunkten und ein besetzter Zustand
in den Quantenpunkten und ein besetzter Zustand ![]() im Leitungsband
benötigt werden,
im Leitungsband
benötigt werden,
| (3.2) |
![\includegraphics[draft=false, angle=270, width=12cm]{bilder/augerskizze.eps}](img591.png) |
Die zeitliche Änderung der Besetzungswahrscheinlichkeit der Quantenpunkte ist, wenn es sich um einen
Auger-Prozeß handelt, gegeben durch die Summation aller möglichen Augerrekombinationen abzüglich der
Summe aller möglichen Stoßionisationen. Jede Wahrscheinlichkeit wird dabei gewichtet mit
![]() beziehungsweise
beziehungsweise
![]() , den Koeffizienten
für Einfang und Emission (Einheiten:
, den Koeffizienten
für Einfang und Emission (Einheiten: ![]() ). Es ergibt sich also
). Es ergibt sich also
wobei die Wahrscheinlichkeit, einen unbesetzten Zustand im Leitungsband zu finden, gleich eins gesetzt wird. Angenommen wird dabei, daß das Leitungsband grundsätzlich nicht voll besetzt ist, also immer geeignete freie Zustände vorhanden sind.
Die zu betrachtenden Halbleiterschichten der Feldeffekttransistoren mit Quantenpunkten sind undotiert, die Zahl der freien Ladungsträger also gering. Für die Nichtentartung läßt sich die Fermi-Verteilung ausdrücken durch
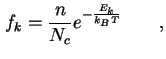 |
(3.4) |
mit den freien Elektronen ![]() und der effektiven Zustandsdichte
und der effektiven Zustandsdichte ![]() [Sch87].
[Sch87].
Diese Besetzungswahrscheinlichkeit eingesetzt in (3.3) ergibt durch Summation über alle
k-Zustände die mittleren Koeffizienten für Einfang und Emission
![]() und
und
![]() ,
,
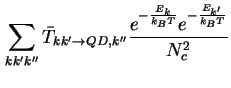 |
(3.5) | ||
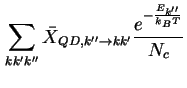 |
(3.6) |
und damit wird (3.3) zu
Im thermodynamischen Gleichgewicht (hier gekennzeichnet durch den Index ,,0``) gilt das Prinzip des
,,detaillierten Gleichgewichts`` (engl. ,,detailed balance``) [Sch87], Einfang- und Emissionsraten
heben sich gegenseitig auf,
Ferner lassen sich die Besetzungswahrscheinlichkeiten für das Gleichgewicht schreiben als Fermi-Verteilung
zum einheitlichen Fermi-Niveau ![]() (
(
![]() : Abstand Energieniveau der Quantenpunkte zum
Leitungsband)
: Abstand Energieniveau der Quantenpunkte zum
Leitungsband)
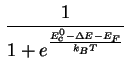 |
(3.10) | ||
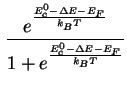 |
(3.11) |
und die Dichte der Elektronen im Leitungsband
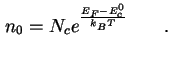 |
(3.12) |
Setzt man dies alles ein in (3.9), so ergibt sich
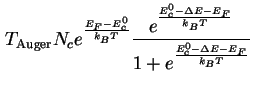 |
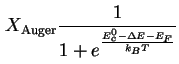 |
(3.13) | |
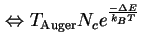 |
(3.14) |
Mit
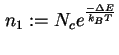 gilt, unabhängig von den Konzentrationen, für die
Koeffizienten von Einfang und Emission der Zusammenhang
gilt, unabhängig von den Konzentrationen, für die
Koeffizienten von Einfang und Emission der Zusammenhang
Unter der Voraussetzung, daß die Koeffizienten der Generations-Rekombinations-Prozesse (gr-Prozesse) konstant bleiben, auch wenn das System aus dem Gleichgewicht gebracht wird, kann (3.15) verwendet werden, um den Koeffizienten der Emission in (3.7) zu eliminieren [Sch87], damit gilt
Der Übergang zur Ratengleichung erfolgt durch Multiplikation von (3.16) mit ![]() (Entartung des Quantenpunkt-Energieniveaus) und
(Entartung des Quantenpunkt-Energieniveaus) und ![]() (Flächendichte der Quantenpunkte). Die Rate der
Prozesse an den Quantenpunkten hat die Einheit Zahl pro Fläche und Zeit. Die Umrechnung der
dreidimensionalen Elektronendichte
(Flächendichte der Quantenpunkte). Die Rate der
Prozesse an den Quantenpunkten hat die Einheit Zahl pro Fläche und Zeit. Die Umrechnung der
dreidimensionalen Elektronendichte ![]() in eine zweidimensionale Elektronendichte
in eine zweidimensionale Elektronendichte ![]() erfolgt durch
Multiplikation mit der Höhe der Quantenpunkte, also
erfolgt durch
Multiplikation mit der Höhe der Quantenpunkte, also
![]() . Dabei wird davon ausgegangen,
daß nur Elektronen aus der Umgebung der Quantenpunkte am Prozeß partizipieren. Es wird (3.16)
zu
. Dabei wird davon ausgegangen,
daß nur Elektronen aus der Umgebung der Quantenpunkte am Prozeß partizipieren. Es wird (3.16)
zu