Bestimmt werden soll zuerst die Ladungsträgerdichte in Quantenpunkten, die so wenig Ladungsträger
speichern können, daß Vielteilchen-Effekte vernachlässigbar sind (vergleiche [Kap00b]). Dafür
werden diskrete Energieniveaus 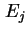 mit Entartung
mit Entartung 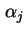 verwendet, die durch Größenfluktuationen
der Quantenpunkte inhomogen verbreitert sind. Die Verbreiterung wird durch eine Gaußverteilung
approximiert mit einem full-width-at-half-maximum (FWHM)
verwendet, die durch Größenfluktuationen
der Quantenpunkte inhomogen verbreitert sind. Die Verbreiterung wird durch eine Gaußverteilung
approximiert mit einem full-width-at-half-maximum (FWHM)
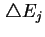 .
.
Nimmt man an, daß die Quantenpunkte im Quasi-Gleichgewicht mit den Elektronen im Leitungsband
sind und mit einer Flächendichte 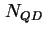 (Einheit:
(Einheit: 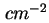 ), einer Dicke
), einer Dicke 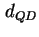 der
Quantenpunktschicht beziehungsweise der Höhe der Quantenpunkte, kann die Dichte pro Volumeneinheit der in
den Quantenpunkten lokalisierten Elektronen geschrieben werden als
der
Quantenpunktschicht beziehungsweise der Höhe der Quantenpunkte, kann die Dichte pro Volumeneinheit der in
den Quantenpunkten lokalisierten Elektronen geschrieben werden als
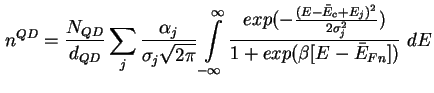 |
(2.7) |
mit
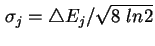 ,
,
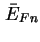 und
und
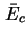 bezeichnen
Quasi-Fermi-Niveau und mittlere Leitungsbandkante im Zentrum der Quantenpunkte [Wet00].
bezeichnen
Quasi-Fermi-Niveau und mittlere Leitungsbandkante im Zentrum der Quantenpunkte [Wet00].
Analog ergibt sich für Löcher
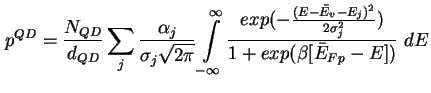 |
(2.8) |
mit der mittleren Valenzbandkante 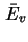 sowie Quasi-Fermi-Niveau
sowie Quasi-Fermi-Niveau
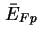 im Zentrum
der Quantenpunkte.
im Zentrum
der Quantenpunkte.
Für Quantenpunkte, die sehr viele Ladungsträger aufnehmen können, findet man in der Literatur als Modell
für die Besetzung die Energieniveaus eines harmonischen Oszillators [Kap00b], [Tar98]. Exemplarisch
soll dieses Modell zur Untersuchung von Ge-Quantenpunkten eingebettet in eine Silizium-Schottkydiode
verwendet werden. Diese Ge-Quantenpunkte haben im Vergleich zu anderen Quantenpunkten eine sehr große
Grundfläche. Man separiert die z-Abhängigkeit der Quantisierung und nähert das Potential über der
Grundfläche durch einen zweidimensionalen harmonischen Oszillator. Die Energieniveaus ergeben sich aus den
Lösungen des harmonischen Oszillators
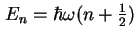 mit jeweiliger Entartung
mit jeweiliger Entartung
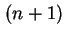 [Lan85], die Dichte der Löcher in den Ge-Quantenpunkten läßt sich schreiben als
[Lan85], die Dichte der Löcher in den Ge-Quantenpunkten läßt sich schreiben als
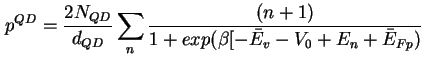 |
|
|
(2.9) |
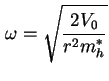 |
|
|
(2.10) |
mit 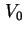 und
und 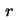 als Tiefe und Radius des harmonischen Potentials (siehe Abbildung 2.4) und
der effektiven Masse der Löcher
als Tiefe und Radius des harmonischen Potentials (siehe Abbildung 2.4) und
der effektiven Masse der Löcher 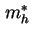 . Summiert wird über alle gebundenen Zustände
. Summiert wird über alle gebundenen Zustände 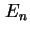 .
.
Abbildung 2.4:
Harmonischer Potentialverlauf.
![\includegraphics[draft=false, width=5cm]{bilder/harmonosz.epsi}](img373.png) |