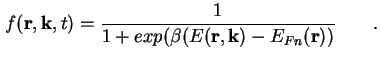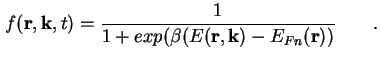Ausgangspunkt zur Herleitung der Strom-Gleichungen ist (A.1) - die Boltzmann-Gleichung [Fer91], [Ash76].
Sie beschreibt die Veränderung einer Verteilungsfunktion
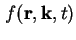 so, daß sich
die Veränderungen durch einwirkende Kräfte (elektrische Felder) im Gleichgewicht halten mit den
Veränderungen durch Relaxations-Prozesse.
so, daß sich
die Veränderungen durch einwirkende Kräfte (elektrische Felder) im Gleichgewicht halten mit den
Veränderungen durch Relaxations-Prozesse.
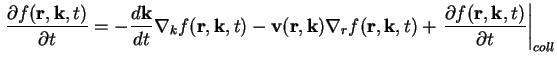 |
(A.1) |
Der Term ganz rechts wird Kollisions-Term genannt, der Rest als Drift-Terme bezeichnet. Die
Boltzmann-Gleichung stammt aus der statistischen Physik [Rei87] und ist wichtiger Bestandteil
der Theorie zur Beschreibung des Transports in Festkörpern.
Unter der Annahme, daß die auftretenden Felder klein sind, werden zur Herleitung desweiteren folgende
Gesetzmäßigkeiten für die Terme in (A.1) - hier für Elektronen - benötigt.
Bloch-Elektronen innerhalb eines Bandes mit einem Wellenvektor k haben eine mittlere
Geschwindigkeit v (Blochgeschwindigkeit) [Ash76]
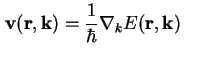 |
(A.2) |
und es gilt ferner
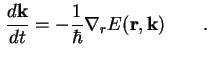 |
(A.3) |
Der Kollisions-Term schreibt sich in der Relaxationszeit-Näherung (relaxation approximation) zu
[Fer91], [Ash76]
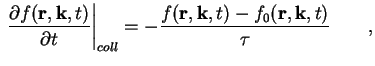 |
(A.4) |
wobei
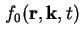 die Gleichgewichts-Verteilung und
die Gleichgewichts-Verteilung und 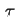 die
Relaxationszeit ist.
die
Relaxationszeit ist.
In dieser Arbeit ist
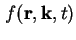 die Fermi-Dirac-Verteilung, hier wieder für
Elektronen (vergleiche auch Kapitel 1)
die Fermi-Dirac-Verteilung, hier wieder für
Elektronen (vergleiche auch Kapitel 1)
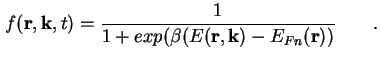 |
(A.5) |
Für die Ableitung der Fermi-Funktion nach r gilt
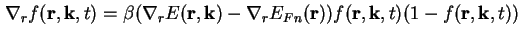 |
(A.6) |
und für die Ableitung nach k
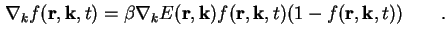 |
(A.7) |