
n basic kos
1997-3-2 last update, 1996-10-27 first day
Robert Jasiek,
jasiek@snafu.de
Copyright: All rights of the author are preserved according to the
international law.
Complexity describes how hard it is to determine all kos on the board and all allowed moves and how long move-sequences in the game can become. In practice with "reasonable" play only move-sequences tend to be short. Complexity is a means of worst case analysis.
Complexity mainly occurs as linear or exponential in the number of board points. Since til today "unreasonable" remains undefined, all ko rule sets at least allow in some "unreasonable" example classes move-sequences of exponential lengths. Sets only considering basic kos allow determination of all kos on the board in linear time. Two simple rule sets of the prohibition class (the Basic Ko Rules and the Prohibition Rules) achieve linear move-sequences in most "reasonable" cases.
Now a few example classes shall be analysed under different rule sets. Assigned complexities describe the lengths of maximal move-sequences leading to repetition. Conventions are defined.

n basic kos
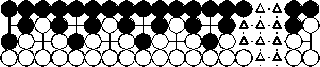
n-tuple ko
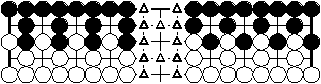
n sending-2-returning-1 of two colours
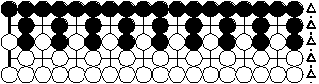
n sending-2-returning-1 of one colour
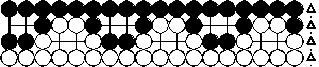
n double ko stones of two colours

n double empty board points of one colour
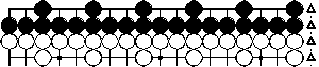
n double empty board points of two colours
Only the Basic Ko Rules and especially the Prohibition Rules partially achieve linearity. The most frequently occuring cases are covered by both.
It is possible to design a set that gains linearity for all shown cases using forbidden suicide. Even then "unreasonableness" of ko strings of at least four stones is not defined. Big ko strings still could hurt linearity even if kos were restricted to small ko strings.
Two solutions exist: