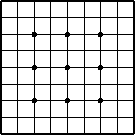
Go ist ein Strategie- und Taktikspiel für zwei Personen. Es wird auf einem Gitterbrett gespielt. Ein Spieler verwendet schwarze Steine, der andere weiße. Sie werden auf freie Schnittpunkte des Gitters gesetzt. Die Spieler sind abwechselnd am Zug, um einen Stein zu legen.
Gitterbrett (hier 9x9 Schnittpunkte)
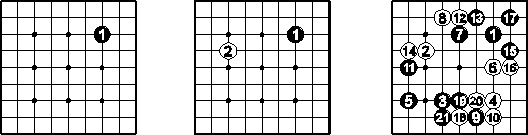
Alternierendes Spiel
Ein Stein oder mehrere Steine einer Farbe, die über Gitterlinien zusammenhängen, bilden eine Kette. Jede Kette muss zu mindestens einem freien Gitterpunkt über eine Gitterlinie benachbart sein. Gegnerische Ketten ohne solchen freien Gitterpunkt werden gefangen. Die somit vom Brett zu nehmenden Steine, die Gefangenen, werden bis zum Spielende aufbewahrt.
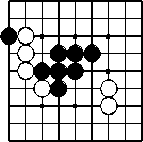
Ketten: 2 schwarze und 3 weiße
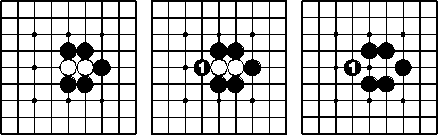
Fangen: der schwarze Zug 1 nimmt der weißen Kette den letzten freien Nachbarpunkt, fängt sie und macht zwei Gefangene
Am Ende eines Spiels gewinnt der Spieler mit mehr Punkten. Es zählen Gebietspunkte und Gefangene. Das Gebiet eines Spielers sind die Gitterpunkte, die von Steinen seiner Farbe umschlossen und damit beherrscht sind.
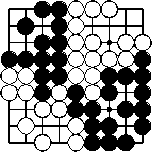
Spielende: die beherrschten Gebiete sind vollständig aufgeteilt
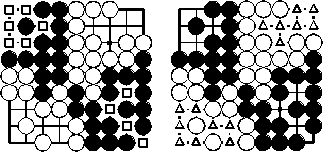
Gebiet: 10 Punkte für Schwarz (Quadrate) - 15 Punkte für Weiß (Dreiecke). Gefangene: Schwarz habe 3 weiße Steine gefangen, Weiß keinen schwarzen Stein. Damit hat Schwarz 10+3 = 13 Punkte und Weiß 15+0 = 15 Punkte. Weiß hat mehr Punkte und gewinnt das Spiel.
Schwarz beginnt das Spiel.
Vor dem Start eines Spiels können sich beide Spieler auf eine Kompensation einigen. Für das erste Zugrecht von Schwarz erhält Weiß üblicherweise 5,5 Punkte, die am Spielende berücksichtigt werden. Eine weitere Möglichkeit räumt dem schwächeren schwarzen Spieler statt eines ersten Zuges die ausgewogene Platzierung von Vorgabesteinen auf den dafür markierten Gitterpunkten ein.
Ein Zug ist verboten, wenn er der Kette des gesetzten Steins nicht mindestens einen freien Nachbarpunkt ermöglicht.
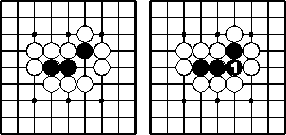
Der Zug 1 ist Selbstmord und verboten.
Ein gesetzter Stein kann auch mehr als eine gegnerische Kette fangen.
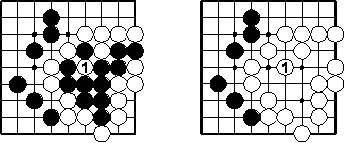
Der weiße Zug 1 fängt zwei schwarze Ketten. (Er ist kein Selbstmord, da nach seiner Durchführung der gesetzte Stein einen freien Nachbarpunkt hat.)
Fängt ein Stein genau einen Stein, so darf der Gegner nicht sofort zurückfangen. Das ermöglicht sinnvolles Spielen.
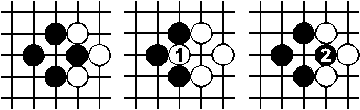
Eine solche Form nennt man Ko. Der Zug 2 ist verboten; er muss woanders platziert werden. Später bekommt Schwarz vielleicht eine Chance, doch noch auf 2 zu spielen.
Meistens wird ein Spieler von seinem Recht, einen Stein zu setzen, Gebrauch machen. Gegen Ende des Spiels ist das nicht immer sinnvoll möglich. Dann kann der Spieler stattdessen sagen, er passe. Das gibt seinem Gegner das Zugrecht.
Alternierendes Spiel kämpft um Punkte. Irgendwann lassen sich die Punktzahlen nicht mehr verbessern. Es werden dann noch die neutralen Punkte besetzt und solche Punkte, auf denen man innerhalb seines Gebiets nachdecken muss. Anschließend passen beide Spieler. Das beendet das Spiel und leitet das Zählen ein.
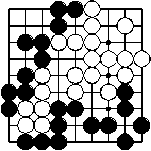
Spätes Spielstadium
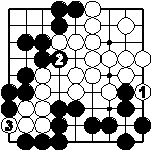
Die letzten Züge des Kampfes um Punkte
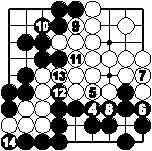
Neutrale Punkte und Nachdecken
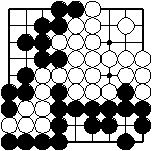
Weiß passt, Schwarz passt. Das Spiel ist beendet.
Es gibt eine gebräuchliche Zählweise. Zuerst werden die Gefangenen in Gebiet ihrer Farbe gesetzt. Dann werden die freien Flächen praktisch umgeordnet (z.B. Zehnerblöcke). Schließlich wird aufsummiert und verglichen.
Spielende
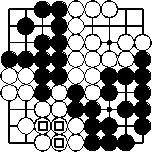
Schwarz' drei weiße Gefangene (Quadrate) werden in weißes Gebiet getan.
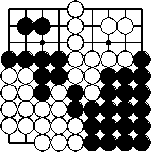
Umordnung in Zehnerblöcke. Schwarz hat 10 Punkte. Weiß hat 12 Punkte und gewinnt.
Ein Spieler kann das Spiel durch Aufgabe beenden.
Nach dem Ende des Spiels und vor dem Zählen wird für jede Kette geprüft, ob sie lebt oder tot ist. Die Steine der toten Ketten werden Gefangene. Alle lebenden Steine verbleiben auf dem Brett. Sie umschließen dann freie Brettpunkte einfarbig. Dadurch ist klar, wem welches Gebiet gehört.
Die Analyse betrifft das Prüfen von Leben oder Tod für Ketten. Sie wird für jede Kette mittels gedachter Fortführung alternierenden Spiels durchgeführt, um zu sehen, ob eine Kette gefangen werden kann. Dabei sind bestmögliche Züge beider Spieler zu berücksichtigen.
Theoretisch kann es sehr viele gedachte Fortführungen geben. Praktisch trifft man bei einer Analyse eine Auswahl, die nur Varianten umfasst, welche Leben und Tod deutlich voneinander abgrenzen. Solche Varianten berücksichtigen die auftretenden Formen in der Umgebung einer Kette. Und sie beginnen alle mit einem Zug des Gegners.
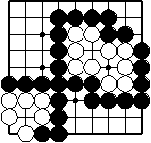Beispiel
1
Die beiden weißen Ketten links unten leben, weil sie nicht gefangen werden können. Warum? Wenn Schwarz eine von ihnen fangen wollte, müsste er damit beginnen, einen der beiden freien Punkte zwischen ihnen zu belegen. Das ist aber Selbstmord und daher verboten. Schwarz hat also niemals die Möglichkeit, eine Variante zum Fangen zu spielen.
Die beiden einzelnen freien Punkte nennt man Augen. Wie man sieht, lebt eine Kette mit mindestens zwei Augen.
Für die weißen Ketten in der Mitte gilt das gleiche: auch sie haben zwei Augen; sie können nicht gefangen werden und leben deshalb.
Was ist nun mit der schwarzen Kette? Sie hat keine Augen im eigentlichen Sinne. Aber wie im Folgenden demonstriert werden soll, kann sie immer zwei Augen bekommen, gleich welche Variante Weiß zum Töten versuchen sollte:
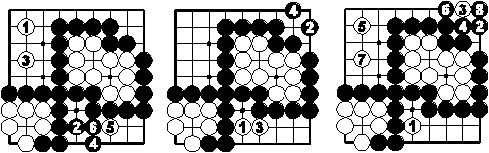3 Varianten
In jedem Fall erhält die schwarze Kette zwei Augen. Sie kann nicht gefangen werden und lebt.
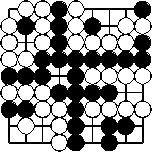Beispiel 2
Die beiden weißen Ketten links oben leben: beide freien Punkte dort sind für Schwarz Selbstmord.
Die beiden weißen Ketten links unten leben auch:
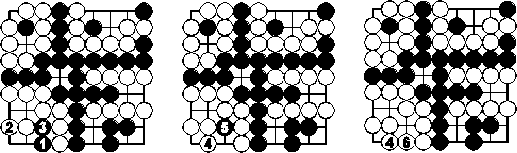Variante 1
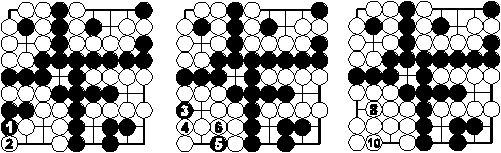Variante 2
Schwarz kann nicht verhindern, dass Weiß zwei Augen bekommt. (In Variante 2 kann Schwarz mit seinen Zügen 7 und 9 praktisch nur passen, da ihm links unten nur noch Selbstmord bleibt.)
Außerdem lebt noch die weiße Kette rechts oben. Eine beispielhafte Variante sei gezeigt:
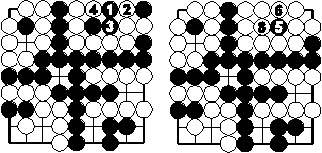
Auch hier bekommt Weiß zwei Augen.
Das Leben der großen schwarzen Kette und der kleinen schwarzen Kette rechts unten sieht man folgendermaßen:
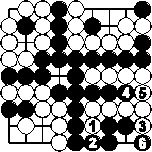
Weiß 1 ist erzwungen; sonst ergibt Schwarz 1 sofort das zweite Auge für die schwarzen Steine. Schwarz 2 sichert die Verbindung und droht für all die schwarzen Steine zusammen mit einem Zug auf 3 einen Raum für ein zweites Auge abzutrennen. Somit ergeben sich die Züge bis zum Fangen mit Schwarz 6, wonach es leicht ist, das zweite Auge zu vollenden.
Somit ist in Beispiel 2 für sieben Ketten erwiesen, dass sie leben, weil sie nicht gefangen werden können - fünf weiße und zwei schwarze Ketten.
Eine Besonderheit des Lebens ist die Koexistenz von schwarzen und weißen Ketten. Sie haben dann keine zwei Augen, aber dafür gemeinsame freie Punkte.
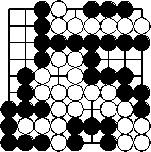Beispiel 3
Auf dem Brett gibt es zwei Koexistenzen. Rechts oben haben die schwarze und die weiße Kette zwei gemeinsame freie Punkte (aber keine Kette hat auch nur ein Auge). Rechts unten haben die schwarze und die weiße Kette einen gemeinsamen freien Punkt und jeweils ein Auge. Die beiden Koexistenzen sind die möglichen Grundformen für gemeinsames Leben. In jedem Fall hat kein Spieler ein Interesse daran, zuerst eine gegnerische Kette töten zu wollen. Er müsste einen gemeinsamen freien Punkt belegen und der Gegner könnte dann sofort die Kette des Angreifers fangen. Also ist kein Fangen möglich, und alle beteiligten Ketten leben.
Bei der Spielauswertung gibt es eine Ausnahme für Koexistenzen: Benachbart zu Koexistenzen gibt es kein Gebiet.
Im Beispiel sind bei der oberen Koexistenz die gemeinsamen freien Punkte kein Gebiet, in der unteren neben dem gemeinsamen freien Punkt auch die beiden Augen nicht.
Das Paradox einer lebenden Kette, die gefangen werden kann ist leicht erklärt: Das Fangen der Kette ermöglicht es einem neuen Stein der gleichen Farbe zu leben. Hier ist ein typischer Fall:
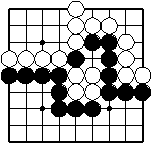Beispiel 4
Der einzelne schwarze Stein kann gefangen werden:
Das führt aber nur zu dem neuen schwarzen Stein 2, der nicht gefangen werden kann. Also lebt der ursprüngliche schwarze Stein.
Eine Kette ist tot, wenn sie nicht lebt.
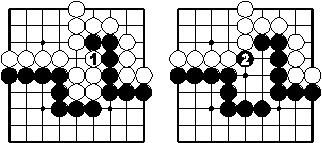
In Beipiel 2 gibt es mehrere Ketten, die tot sind: all diejenigen, die nicht leben. Hier wird nun anhand einer großen toten Kette (der weißen rechts unten) gezeigt, wie sie gefangen werden:
Weiß kann sich kaum wehren und passt daher. Schwarz füllt die freien Nachbarpunkte. Das zeigt den Tod der weißen Kette rechts unten (und nebenbei den der weißen Kette darüber).
Die vier kleinsten schwarzen Ketten sind ebenfalls tot - Weiß kann jede von ihnen fangen.
Beispiel 5
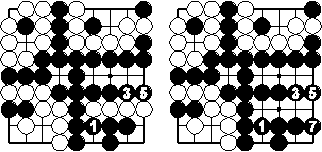
Die weiße Kette ist tot; das soll nun gezeigt werden:
Schwarz nähert sich von außen an. Weiß macht einen kurzen Versuch der Gegenwehr mit dem Zug 2, um ein Auge zu drohen, aber Schwarz 3 verhindert das. Die Annäherung von außen geht weiter bis Schwarz 15 (während Weiß immer passt). Nun könnte man die Stellung für eine Koexistenz halten. Aber der Schein trügt:
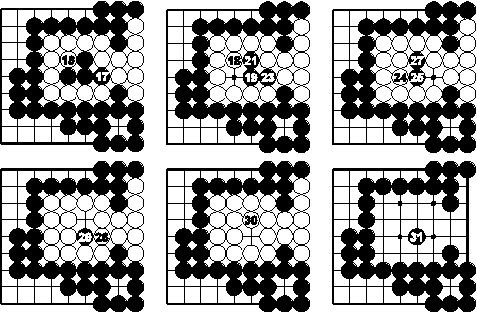
Schwarz nimmt nun den Raum für Augen von innen. Jedesmal, wenn Weiß nur noch einen freien Nachbarpuinkt hat, verschafft er sich anderen Freiraum durch Fangen. Jedoch wird der Raum kontinuierlich kleiner. Und Schwarz beginnt das Zusetzen neuen Freiraums immer so, dass Weiß ihn danach nicht in zwei Teile für zwei Augen aufteilen kann. Schließlich ist Weiß gefangen. Das zeigt, dass die ursprüngliche weiße Kette tot ist.
(Die ursprüngliche schwarze Kette in der Mitte kann zwar gefangen werden, aber das ermöglicht letztendlich nur einen neuen schwarzen Stein, der nicht gefangen werden kann. D. h. die Kette lebt.)
In der Analyse gilt für jedes Ko: Fängt ein Spieler in dem Ko, so muss der Gegner erst für dieses Ko passen, bevor er zurückfangen darf. Das bedeutet, dass der Gegner passt und dabei ein Ko benennt. Meistens ist danach das Ko schon aufgelöst, bevor die Chance zum Zurückfangen im nächsten Zug des Gegners realisiert werden kann. Die Kette eines solchen Kos ist tot.
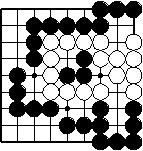
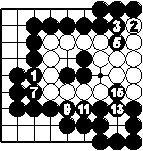
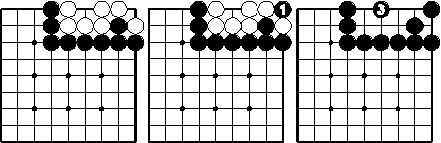Beispiel 6
In der rechten oberen Ecke ist ein Ko. Schwarz 1 fängt in dem Ko. Weiss will verhindern, alle Steine zu verlieren, und passt deshalb mit Zug 2 für das Ko rechts oben. Schwarz 3 aber löst das Ko auf, indem auch noch die letzte weiße Kette gefangen wird. Damit kann Weiß kein Ko mehr zurückfangen. Auch ist ersichtlich, dass die ursprünglichen weißen Ketten tot sind.
Sobald man in der Analyse alle toten Ketten bestimmt hat, sind sie zu entfernen. Sie werden Gefangene, und das nun deutlich ersichtliche Gebiet ist zu zählen.
Tote Ketten sind schon allein durch die gedachte Fortführung alternierenden Spiels gegeben. Das bedeutet, ein Annähern und sogar Fangen solcher Ketten durch alternierendes Spiel vor dem Spielende ist überflüssig. Ja, es ist sogar unklug. Mit jedem tatsächlich gespielten Annäherungszug setzt man einen Punkt zu. Solche Punkte zählen dann später bei der Auswertung nicht mit, da sie nicht mehr frei sind. Sie gehen verloren.
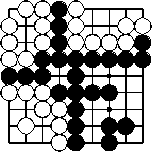
So sieht Beispiel 2 nach dem Entfernen der toten Steine aus. Weiß hat dabei fünf weitere Gefangene gemacht, Schwarz acht. Nun kann gezählt werden.