| |
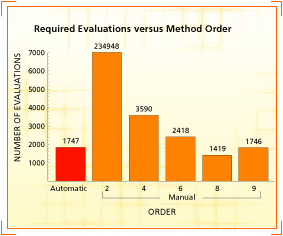
The chart compares the number of
evaluations required to solve a particular ODE with different orders
of Runge-Kutta method. Although Mathematica's full automatic
algorithm selection produces a near-optimized result, selecting 8th
order will in this case be more computationally efficient. However,
guessing the best order to use--as required in non-Mathematica,
manual-only systems--would typically be highly inefficient.
|
 |
Setting a selective method override in a Mathematica function
means manually narrowing down how Mathematica should carry out
the computation to a particular method or class of algorithms, though
not its order or sub-algorithm. This is a halfway point between
letting Mathematica automatically select the best option
using AAS or manually specifying
everything.
For example, ExplicitRungeKutta
is a selective method override specifiable in the numerical
differential equation solver NDSolve. Choosing
it enables all the different orders of Runge-Kutta methods to be
utilized under AAS control but prevents the use of other methods, such
as Adams or BDF.
|  |


