
1998-09-14 last update, 1998-08-24 first day, jasiek@snafu.de
In June 1998 the international mailing list "go-rules" at go-rules@usgo.org has sincerely discussed international rules and decided to contribute to creation of unified go (igo, weiqi, baduk) rules that shall be suitable for international usage. Thereby created rule texts and comments are presented on this page.
A play may not recreate a previous board position from the game. This refers to the position just after the play and any consequent removals.
[Replace the "Move" section by the following:]
A play causing a remaining own region to be without any adjacent empty intersections is prohibited.
[Replace the "No Repetition" section by the following:]
[Replace the "Scoring" section by the following:]
International rules shall have the following aims:
Most obviously, international rules must be suitable for international play. This especially includes international events. - Everybody wants to promote the game throughout the world. This is done by people and entities rather than rules. However, a clear and unified set of rules can make promotion only easier rather than stirring up unnecessary problems.
Simplicity ensures that everybody knows the rules or has easy access to them, and that they are understood and can be applied easily. On the other hand, exceptions would be hard to remember and to understand and cause superfluous trouble. - Completeness allows immediate application of the rules for any board position. Thereby quarrels, which might arise otherwise, are avoided. - Correctness means that the rules themselves do not contain any contradiction, which would hurt their fair application.
Rules for the game should describe it and nothing else. History has seen slight regional differences, however, the nature of game is virtually the same everywhere. Unification of the rules requires changes of prior rule sets. For a consensus some regional details must be modified to achieve international acceptability.
The international rules are devided into
This distinction is very useful since the core rules of play describe the essential features of the game, which cannot be omitted, while tournament rules describe everything else, which is considered useful but can be changed or amended more easily. The core rules of play specify what a legal game and its outcome is. Additions are left for tournament rules.
The core rules of play are offered as a basic rule text together with three alternatives for parts of it. The basic rule text itself is complete and the alternatives could be simply ignored. However, in view of a final creation of a unified international rule text, it is hard to predict whether an alternative might be preferred or not. Therefore the alternatives are given to allow for an easy choice among ready texts. After a choice no alternatives will remain. - The wordings of all texts have been formulated very carefully.
The core rules of play have their general part which introduces the board and general definitions. There are countless possibilities of introducing general definitions for the game. The ones chosen in the rule text use words of natural language, can be understood easily, and be grasped visually. Besides the expected terms "game", "player", "board", and "stone" they especially include "intersection", "adjacent", "connected", and "region". Most doubtful, confusing, and superfluous terms like "life" and "death", which refer to game tree analysis, do not occur.
The most essential sections of the rules are "Move", "No Repetition", and "Scoring". "No Repetition" is sometimes referred to as "Ko", but "No Repetition" not only gouverns special ko shapes but prohibits repetition in any case. So the term "ko" is redundant. The "score" defines which points determine the win. In contrast, "counting" methods are mechanical procedures that can vary in every game without changing the score definition. For this reason, "counting" belongs to tournament rules while "scoring" is a necessary part of the core rules of play.
In theory, after alternation two passes could simply end a game. However, mostly some kind of agreement option just before the end of a game is applied. Therefore the basic rule text also includes an "Agreement" section that describes removals due to an agreement between the players.
The first alternative affects "Suicide" respectively "No Suicide". Arguments in favour of either choice could be retrieved and it is not utterly obvious whether one is superior.
The second alternative concerns "No Repetition". The two choices are
The simple choice without exception is "no recreation of previous board positions". The other choice describes the most frequent special basic ko case and other cases that then still may recreate previous board positions only to lead to confusing options of exceptional game ends. Except for mere tradition it is not clear why one should avoid the simple and general choice. Regional tradition is hardly a better advice for a unified no repetition ruling than a simple and clear rule.
The third alternative is about scoring. The two offered choices are a) area scoring and b) equivalence scoring:
Traditionally, further scoring methods are known (especially traditional territory scoring). However, they refer to the whole game tree, are incomplete, are difficult to apply, and include exceptions. They would fit none of the aims of simplicity, completeness, and correctness.
Area scoring is the simple choice as it is a single scoring method. Equivalence scoring uses either area scoring or a modified version of territory scoring. The major modification is the inclusion of a compensation of one prisoner for each pass. In practice, this affects only about three moves of a game. But as a consequence, equivalence scoring is a unification of both major scoring systems in the world. So while equivalence scoring is conceptionally a little more difficult than just area scoring, it is a good candidate for a world-wide compromise.

The board: A grid of 19 horizontal and 19 vertical lines forming 361 intersections.

An intersection is marked with a triangle.
Four intersections have a black stone, three a white stone, all other no stone on them.
The two marked intersections are adjacent.
Three marked examples of adjacent intersections.
The marked intersections are connected because they are both black and adjacent to each other.
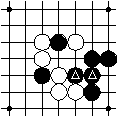
The marked intersections are connected because they are both black and adjacent to each other.
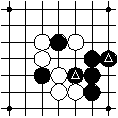

The marked intersections in the left diagram are connected because they are both black and there is a chain of black intersections between them, as shown in the right diagram.
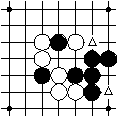
The marked intersections in the left diagram are connected because they both have no stone on them and there is a chain of intersections without stones on them in between, as shown in the right diagram.
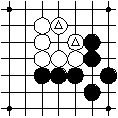

The marked intersections in the left diagram are connected because they are both white and there is a chain of white intersections between them, as shown in the right diagram.
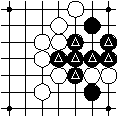
The marked black intersections are a region.
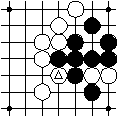
The single marked white intersection is a region.
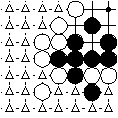
All the marked intersections without stones on them are a region.
Scores are measured in "points" to avoid any confusion with "intersection". - A "region" can be black, white, or empty. Thus one does not need the two terms "string" and "territory" and thereby avoids any trouble in connection with words like "chain", "army", or "group" for "string" and "area" for "territory".
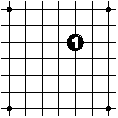
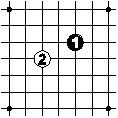

The players move alternately, with black starting.
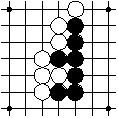
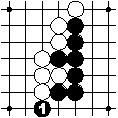
This is a move of the black player that is a play of a stone on an empty intersection.
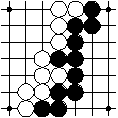

This is a move of the white player, e. g., that is a pass.
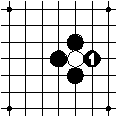

The black play causes the white region to be without any adjacent empty intersections. Therefore the stone of this region is removed.

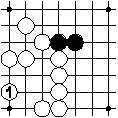
The white play causes one black and one white region to be without any adjacent empty intersections. Some region has to be removed. Removing opposing regions takes precedence over removing own regions. Therefore the black region in question is removed. Then each region of stones has some adjacent empty intersections and the play is finished.
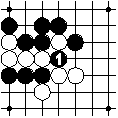

The black play causes two white regions to be without any adjacent empty intersections. These regions are removed.
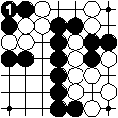
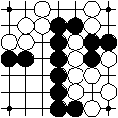
The black play causes one black region to be without any adjacent empty intersections. This region is removed.
The rule "A play may not recreate a previous board position from the game." is also known as positional super ko rule.
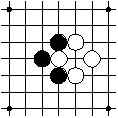
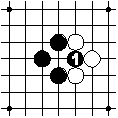
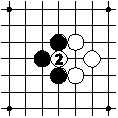
The white play at 2 would recreate the board position before the play 1. Therefore the play 2 is prohibited and must be done elsewhere for the time being.


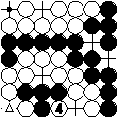
Black mistakenly plays at 1 and removes one stone. Then white cannot remove 1 since this would recreate the board position before 1. Thus he plays 2. Now black cannot play to remove 2 since this would recreate the board position before 2. So the black move 3 is a pass. Now that no black stone is in the lower left corner, white can play 4 without violating a rule. But finally, black cannot play 5 at triangle because it would recreate the board position before 1. Therefore black should not have used his move 1 for a play but passed instead, followed by a white pass.
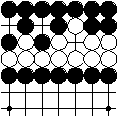
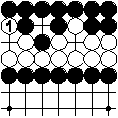
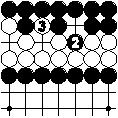
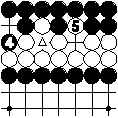
After white 1 black cannot play to remove 1 immediately, so black should play on another part of the board. He could also decide to continue with 2, etc. However, after 5 he can neither play to remove 5 nor play at triangle, which would recreate the board position before move 1. So black is forced to play on another part of the board (or pass) anyway.

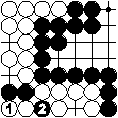

White should pass. If he still plays, he cannot play at triangle after 2 since this would recreate the board position before 1.
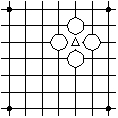
Black cannot play at triangle and remove the just created black region of one stone because the play would only recreate the board position.
In theory, alternation of moves could simply end with two successive passes and be followed by scoring immediately. However, most players in the world are used to perform removals just before scoring due to verbal agreements rather than alternate moving. For this reason, an agreement option is included.
As soon as two successive passes occur, the players may make an agreement. Normally, they agree, remove accordingly, and score the game.
The players may disagree and continue alternation. In this case no removals take place for the time being. Later, when two successive passes occur again, the players have the agreement option again. Only once in a game the players can actually perform removals due to an agreement. Right after that the game is scored. Thereby no confusion due to restored positions or partial removals can arise.
For an agreement the players designate regions that shall be removed. Obviously, only black or white regions can be removed at all. Each region can be removed as a whole only. (There would be no need for partial removals.)
In case of a disagreement, the players continue alternation as if the last two successive passes had not occured, i. e. the opponent of the last passing player starts continuation. - If then both players just pass, the game ends with scoring immediately. So the players cannot avoid scoring by passing and disagreeing forever.
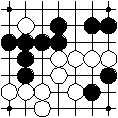
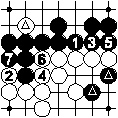

From the actual position in the left diagram the players go on with the move alternation as in the middle diagram. Then white 8 is a pass and black 9 is a pass. This stops alternate moving. Now the players make an agreement. They agree to remove the three marked regions but none else. Then they remove these three regions. This ends the game as shown in the right diagram. Finally, the game will be scored.



In the left diagram white 1 passes and black 2 passes. Then the players attempt an agreement. Black suggests that all marked regions shall be removed. White disagrees. So alternate moving continues with white as the opponent of the last passing player. White 3 is a pass. Then moving continues as shown in the middle diagram. Not shown are the moves white 5 passes; white 7 passes; white 9 passes; white 11 plays at A, black 12 plays at B, white 13 passes, black 14 plays at 10, white 15 passes; white 17 plays at C, black 18 plays at D, white 19 passes, black 20 plays at 16, white 21 passes; white 23 passes, black 24 passes. Two successive passes have occurred again introducing a new possibility for agreement. This time both players agree that no region shall be removed and the board position in the right diagram is used for scoring.
The scoring method, which is also known as area scoring, scores for each player all intersections with his stones and the intersections of the empty regions that are only adjacent to intersections with his stones. Hence the board position and nothing else is used for scoring.

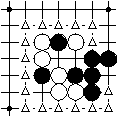
In this scoring position 13 points score as black intersections for black, 11 points score as empty intersections for black, 13 points score as white intersections for white, 12 points score as empty intersections for white. Altogether, the black score is 24 points, the white score is 25 points. White has more points and wins the game.
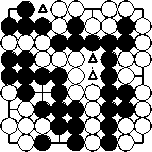
In this scoring position the three marked intersections belong to empty regions that are adjacent to intersections with black as well as white stones. Therefore they do not provide points for the scores. 34 points score as black intersections for black, 3 points score as empty intersections for black, 35 points score as white intersections for white, 6 points score as empty intersections for white. Altogether, the black score is 37 points, the white score is 41 points. White has more points and wins the game.

The black play would cause one black region to be without any adjacent empty intersections. This is prohibited; black cannot play at 1.



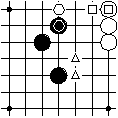
The white play at 2 would remove the single stone of the last preceding play 1 that has removed a single stone itself. This is prohibited, so the play 2 must be done elsewhere for the time being.



White 2 cannot remove black 1 that is the last preceding play and has already removed a single stone. So white plays 2 as shown. Now black 3 cannot remove 2 due to the same rule and therefore passes. If white 4 also passed and both players then agreed to end the game, the position would virtually be the same as before move 1. If white 4 also passed and both players then disagreed, then the game would continue with black and he would face the same prohibition for his play since the last preceding play 2 does not allow a removal of the stone 2, so nothing changes. - If 4 continues as shown, then black will play 5 at triangle. Now other rules become active, those that watch recreations of previous board positions. Between both occurrences of the board position in question two black and two white stones have been removed. The difference of both stone numbers is zero. This means that the game then exceptionally ends without result. Hereby the result of the game is "no result". - If black does not like the exceptional game end without result here, he might pass instead of his move 1. And if then white removes a stone, forcing black to remove a stone, white then passes, then black can pass to achieve a regular game end. - If white does not like the exceptional game end without result here, he might pass instead of his move 4 to achieve a regular game end. - To summarize, the initial position should be met by both players with passes. Only if both unreasonably cooperated, the game could be without result.




The move sequence from 1 to 5 is forced due to prohibited immediate removals of single stones. Next black will play at triangle invoking the rules about recreation of previous board positions. Until then three black and three white stones will have been removed. The difference is zero. Therefore the game exceptionally ends without result then.



White should pass. If he still plays and uses 3 at triangle to recreate the board position before 1, then between both its occurrences one black stone and two white stones have been removed. The difference is not zero. So the game exceptionally ends with a win of black who is the player with fewer removed stones. Thus in practice such a move sequence is likely to be omitted and passes are used instead. The according rule about an exceptional win is needed to disable a player to avoid losing by disturbing forever. (Note that under territory scoring after the play 3 black 4 would pass and spend one pass stone. This results in two black and two white prisoners during the move sequence from 1 to 4.)

Black is not well advised to play at triangle. This would recreate the board position and one black stone would be removed in between. Hence the game would exceptionally end with a white win since fewer white stones are removed. (A no suicide rule would even explicitly forbid self-removal of a single stone.)
Equivalence scoring allows to score either area or territory, which are equal. In both cases the empty regions only adjacent to intersections with own stones contribute to the score. Additionally, while intersections with own stones are included in the area of each player, territory uses the prisoners that are opposing stones instead. Thus to enable territory scoring as well, prisoners must be handled properly during the game.


One of the prisoners' sources is removals during alternation. In this example, the one removed white stone is added to the prisoners.
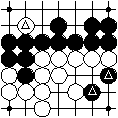

Another source is removals due to an agreement after two successive passes. The diagrams illustrate two removed black stones and one removed white stone. They are added to the prisoners.
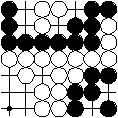
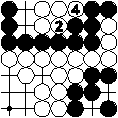
Black to move in the left diagram passes his move 1 and adds one black stone to the prisoners. White moves at 2 followed by a black pass as his move 3. Again one black stone is added to the prisoners. Black 5 is yet another pass causing one more black stone for the prisoners. Then white 6 is a pass and white adds one white stone to the prisoners. White already passes as the last player here.



White to move. White passes adding one white stone to the prisoners. Then black passes adding one black stone to the prisoners. The game stops. Then the players agree that no region shall be removed. Now the game is just before scoring. So far the last passing player has been black. However, the last passing player has to be white. Therefore white makes an extra pass and adds one further white stone to the prisoners. Hence the number of black and white moves throughout the game is equal. This validates equivalence scoring.

Area scoring: The score for each player is given by all intersections with his stones, and the intersections of the empty regions that are only adjacent to intersections with his stones. In this scoring position 13 points score as black intersections for black, 11 points score as empty intersections for black, 13 points score as white intersections for white, 12 points score as empty intersections for white. Altogether, the black score is 24 points, the white score is 25 points. White has 1 point more and wins the game.
Territory scoring: The score for each player is given by the intersections of the empty regions that are only adjacent to intersections with his stones, and the prisoners that are opposing stones. During alternation no stones have been removed. However, during agreement two black stones and one white stone have become prisoners. Before the agreement each player has passed once and thereby added one stone each to the prisoners. During this successive passing white has passed first, black last. Therefore, after the agreement and just before scoring, white has made an extra pass adding another white stone to the prisoners. So there are 0+2+1 = 3 black prisoner stones and 0+1+1+1 = 3 white prisoner stones. (In practice, these would be kept aside the board and could be watched easily.) Now to the scores: 11 points score as empty intersections for black and 12 points score as empty intersections for white. Altogether, the black score is 11+3 = 14, the white score is 12+3 = 15. White has 1 point more and wins the game.
Equivalence: Area and territory scoring are equal: they both score a 1 point win for white. (This is not surprising: It follows from the equivalence proof .)
Equivalence scoring is designed in a way that equals area scoring and territory scoring. This is ensured by the usage of pass stones and white passing last. But the most essential fact is that each single prisoner stone under territory scoring scores one point more for the opponent of the stone's colour, and at the same time under area scoring this missing stone on the board scores one point less for the player of the stone. The formal proof requires some mathematical intricacies and is offered for the interested reader and as a final means of verification.
Area scoring and territory scoring are equal in the international rules of play with equivalence scoring.
Let for b,w = black, white be the following point numbers:
By definition, area scoring is Ab - Aw, territory scoring is Tb - Tw.
Then the theorem can be written as
This is the equation that is to be verified.
Facts:
Reasonings for facts:
Transformation starting from a truth:
| (2) | Mb = Mw |
| <=> | Mb - Mw = 0 |
| <=> | (Mb - Mw) + (Pw - Pb) = Pw - Pb |
| <=> | (Mb - Pb) - (Mw - Pw) = Pw - Pb |
| <=(3),(4)=> | Sb - Sw = Pw - Pb |
| <=> | (Sb - Sw) + (Rw - Rb) = (Pw - Pb) + (Rw - Rb) |
| <=> | (Sb - Rb) - (Sw - Rw) = (Pw + Rw) - (Pb + Rb) |
| <=(5),(6),(11),(12)=> | Ob - Ow = Xw - Xb |
| <=> | (Ob - Ow) + (Eb - Ew) = (Xw - Xb) + (Eb - Ew) |
| <=> | (Ob + Eb) - (Ow + Ew) = (Eb + Xw) - (Ew + Xb) |
| <=(7),(8),(9),(10)=> | Ab - Aw = Tb - Tw |
| (1), q.e.d. |
Tournament rules can cover many topics: Amendments to the core rules of play (like resignation, how to play a stone, result agreement), counting, compensation, conditions of play (like thinking times, schedules, adjournment, playing sites), equipment specifications, organization and execution of events (tournaments, matches, etc.), rights and duties of entities, tournament systems (e. g. knock-out, MacMahon, round-robin) and their details (like number of rounds, winning criteria), jurisdiction, penalities, ranks and ratings, participation, conduct, prizes, sponsoring, dealing with language barriers (e. g. indicating a pass or a region to be removed), etc.
There is much scope for specifications of tournament rules. The presented text only treats a few rather important issues and may serve as a starting point for further discussion. In general, the current text tends to be liberal.
It is of little importance which counting method is applied. A game's result is determined only by the score. One can choose various counting methods. The text allows a choice and includes some precise descriptions of the most useful counting methods. This is helpful for not every counting method is familiar to everybody. The present descriptions are kept simple and do not include handlings of komi or possible handicap recompensations. It should be noted that counting methods must fit the selected scoring type.
The methodically simplest counting methods are point by point counting for area scoring and stone counting for area scoring. Point by point counting for area scoring has been applied together with New Zealand rules. Its main advantage is the included result check. In ancient times stone counting was applied together with stone scoring. It has rarely been applied for area scoring so far. This is a little strange since it can even be used by people who cannot count numbers.
The fastest counting method probably is point by point half counting for area scoring. No point by point counting method requires any rearrangment of stones. So for this no time is consumed. Also the scoring position is not disturbed and a result reconfirmation can be done easily; cheating is out of the question. Half counting methods refer to only one player's points and hence are fast.
The traditional counting methods are Chinese half counting for area scoring and Japanese counting for territory scoring. Either is very sophisticated and complicated due to much rearrangement of stones. These methods were invented to make use of the decimal system as far as possible.
Every counting method has various advantages and disadvantages. Therefore it is suggested to leave the selection of a suitable method to tournament organizers or players.


Point by point counting for area scoring: The 24 squared intersections score for black, the 25 triangled intersections score for white. White has 1 point more and wins the game. (A result check is possible: 0 intersections belong to empty regions that are adjacent to both black and white intersections. The board has 49 intersections. 24+25+0 = 49 is correct.)

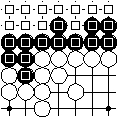
Point by point half counting for area scoring: 0 intersections belong to empty regions that are adjacent to both black and white intersections. The board has 49 intersections. The difference of 49 and 0 is 49, half of it is 24.5. This is the reference point for the half count. The 24 squared intersections score for black This is 0.5 points less than the reference point. Thus white has more points and wins by 2*0.5 = 1 full count point.



Stone counting for area scoring: The empty region only adjacent to black intersections scores for black and is filled with black stones. The empty regions only adjacent to white intersections score for white and are filled with white stones. Then pairs of one black stone and one white stone are taken off the board as long as possible. 1 white stone remains on the board. Thus white wins by 1 point.


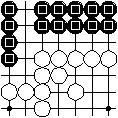
Chinese half counting for area scoring: The empty region only adjacent to intersections with black stones is rearranged to fit a multiple of ten. For this purpose one black stone is additionally used for filling one of the region's intersections. From then on the number of black stones on the board remains constant. The empty intersections counting for black are triangled and add up as 10. Now the black stones on the board are rearranged in multiples of ten as far as possible. There are 14 black stones. The black points for the half count are 10+14 = 24. The board has 49 intersections. 0 intersections belong to empty regions that are adjacent to both black and white intersections. The difference of 49 and 0 is 49, half of it is 24.5. This is the reference point for the half count. Black has 0.5 points less than the reference point. Thus white has more points and wins by 2*0.5 = 1 full count point.


Point by point counting for territory scoring: There are 3 black and 3 white prisoners. 11 intersections of an empty region only adjacent to intersections with black stones score for black. 12 intersections of empty regions only adjacent to intersections with white stones score for white. Opposing prisoners are added: Black's score is 11+3 = 14, white's score 12+3 = 15. White has 1 point more and wins the game.

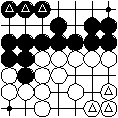

Japanese counting for territory scoring: There are 3 black and 3 white prisoners that are put in respective regions that score for the according player. Then the regions that score for either player are rearranged in multiples of ten as far as possible. During this procedure stones can be shifted appropriately between regions scoring for the same player. Then the intersections for black resp. white are counted. Black has 8 points, white has 9 points. (There are no remaining prisoners any more.) White has 1 point more and wins the game.
During this century, komi values are in general slow increasement. For this reason, a single value is not prescribed. - In international play most games can be expected to be even games. So handicap stones are a minor issue and both major systems (free resp. fixed handicap) are listed. - The text about overtime has been restricted to the most popular system of overtime periods.
(Please excuse the appearence of the diagrams; my server space is restricted and the go diagram editors are insufficient.)