
the board consisting of 19x19 points connected by lines

the board consisting of 19x19 points connected by lines
Other board sizes are conceivable: 9x9, 13x13, 17x17, 21x21.
A path connects two points of the graph along lines. A path can be directed from one point to the other.
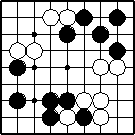
the colours
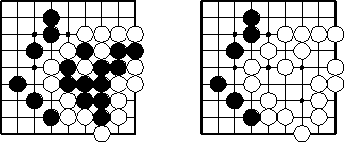
A position ("board position", "colouring", "configuration", "board configuration") of the graph is the colours of all points. The diagram is an example position. (Sometimes a position in contrast to a configuration has no surrounded stone.) A situation of the graph is a position together with the information which player follows next in alternation according to a move rule ("right to play").
Normally go is played between two players. One player is identified with black, the other with white. Each player uses his colour and wins or loses due to the final distribution of his colour on the graph. Either player is called the opponent of the other player.
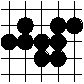
connection
In the example all black points are connected. Not all empty points are connected, but two subsets of empty points are connected and separated by black points.
A black respectively white connected subset is called string (or "chain" or sometimes and less reasonably "group"). An empty connected subset is called region ("area", "territorial region", "territorial area"). Depending on context string or region may be maximally or not.
A black / white point is surrounded if no leaving path reaches empty first after black / white; an empty point is surrounded by black / white if any leaving path reaches black / white first after empty. A surrounded point is always part of a connected subset of the graph.
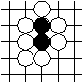
surrounded black string
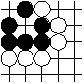
surrounded empty points
In the first example the black string is surrounded by white. In the second example the two empty points in the upper left are surrounded by black, all other empty points are surrounded by white.
A liberty ("breath") of a black respectively white point is an empty point with a line between both. A liberty of a string is a liberty of one of its stones.

liberties
In the example the single white stone on the upper side has exactly one liberty right of it. Both black strings have two liberties each.
A removal ("capture", "emptying", "clearing") as to black respectively white is the colour change to empty for all surrounded points of the colour. All strings of the colour without a liberty are removed due to rules.
removal of black
A prisoner is a removed stone.
Sometimes a setup called handicap may be used instead of a normal start.
A free handicap of N points is a black colouring of N arbitrary but different points of the graph. (This is N - 1 more than normal.)
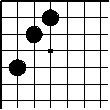
free handicap with N = 3
A Japanese handicap of N points is a black colouring of N fixed points of the graph. (This is N - 1 more than normal.)
Japanese handicap
The European application of Japanese handicap is as follows depending on N (the black player sitting below the board):
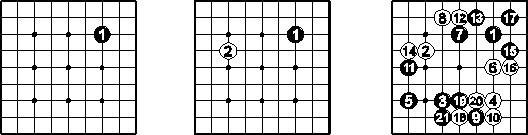
board plays

pass play: black announcing "pass"
Alternative terms for move / board play / pass play are move / play / pass or less common play / move / pass, turn / move / pass. So "move" depends on context.
Suicide is removal of stones of the moving colour. Move rules may allow or forbid suicide. If suicide is allowed, then removals of opponent's stones precede those of own stones. Else the former may never lead to the possibility of the latter.
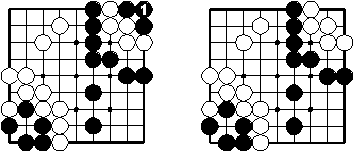
suicide and caused removal
Shapes occuring in cyclical play are sometimes called "ko", but definitions strongly vary between rule sets. The following terms are necessary for study of prohibition rule sets.
A cycle is a finite move-sequence so that the positions before and after it are the same. A cyclical move-sequence is a cycle with board plays only.
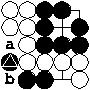
cycle
A cycle is black a - white b - black triangle - white pass. (Also black a - white b - black triangle is a cycle, but a cyclical move-sequence, too.)
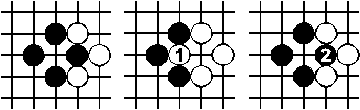
cyclical move-sequence consisting of two board plays
First one thought that it be suitably possible to define a term "ko string" (and each stone of it as "ko stone") for prohibition rule sets. In the meantime, a mathematical definition has been given that clearly shows the impossibility of a practically useful definition. Simply speaking, one calls the strings captured in a cycle ko strings. Since this makes any string a ko string, the following definition has become necessary: